相对面教育同步相对面教育备考资料信息：2024年国省双考公务员备考:09-14每日一练:数量关系之几何问题。更多关于国家公务员考试，安徽公务员考试，安徽事业单位备考，安徽公务员考试资料等相关资讯，请关注相对面教育的备考资料，以及安徽相对面教育(www.xduim.com)官网和考务咨询热线(0551-63644001)，获取更多招考信息和备考资料。

数量关系之几何问题

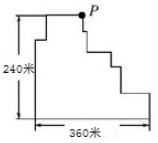
1、如图是某学校操场平面图，甲每天放学后，都会围着操场跑步，已知甲每天跑三圈，花费10分钟，则甲跑步的速度为多少米/秒？
       

A、2

B、6

C、180

D、360

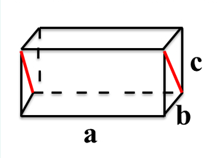
2、沿一个平面将长、宽和高分别为8、5和3厘米的长方体切割为两部分，问两部分的表面积之和最大是多少平方厘米？

A、206

B、238

C、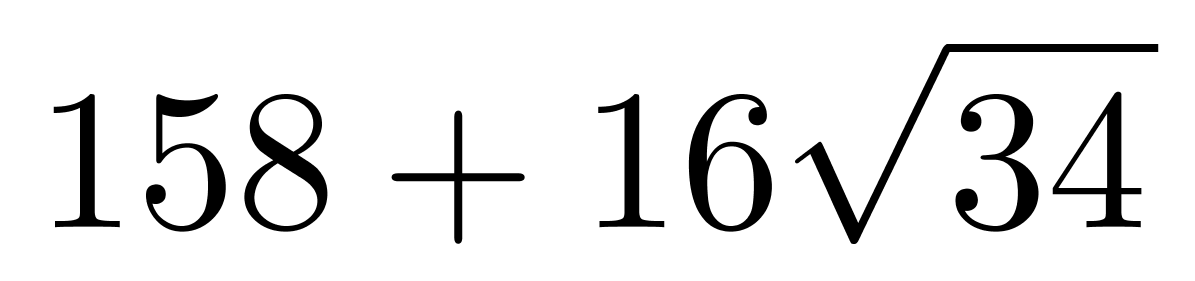

D、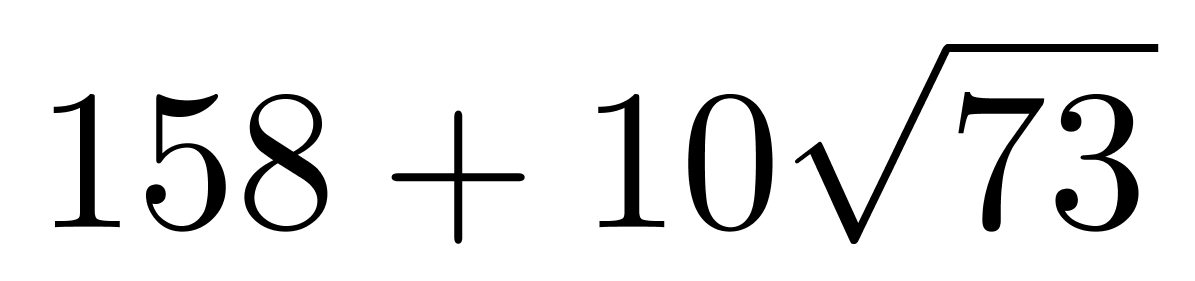

3、如图，甲、乙、丙、丁四个长方形拼成正方形EFGH，中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是，四边形ABCD的面积是。问甲、乙、丙、丁四个长方形周长的总和是：
       

A、32cm

B、56cm

C、48cm

D、68cm

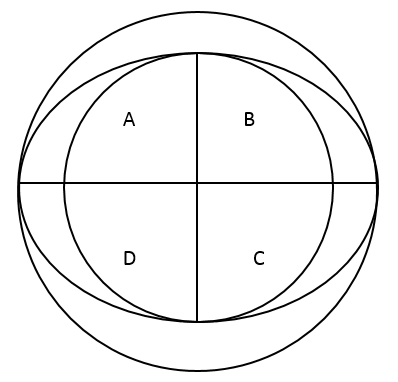
4、有一个椭圆型的花坛以长短轴划分成了ABCD四个相等大小的部分，分别种了月季花、玫瑰花、狗尾巴花和玫瑰花，现已知长短轴分别为16米和12米。问花坛中玫瑰花的面积为多少平方米？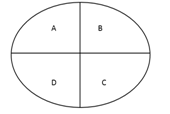

A、24π

B、36π

C、48π

D、64π

5、一个扇形的面积是314平方厘米，它所在的圆的面积是1256平方厘米，则此扇形的圆心角是：

A、180°

B、60°

C、240°

D、90°

【参考答案及解析】

1、

       第一步，本题考查几何问题。
       第二步，平移图中线段，平移拼接起来就是长360米，宽240米的矩形（如右图所示），所以甲跑步的总路程为（360+240）×3×2=3600（米），则速度为3600÷10=360（米/分钟），即6米/秒。
       因此，选择B选项。
       

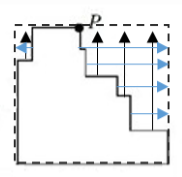
2、

第一步，本题考查几何问题，属于立体几何类。
第二步，两部分表面积之和由长方体表面积和两个切面面积构成。要使两部分表面积之和最大，使切面面积最大即可。沿不同的对角线切割后，切面面积有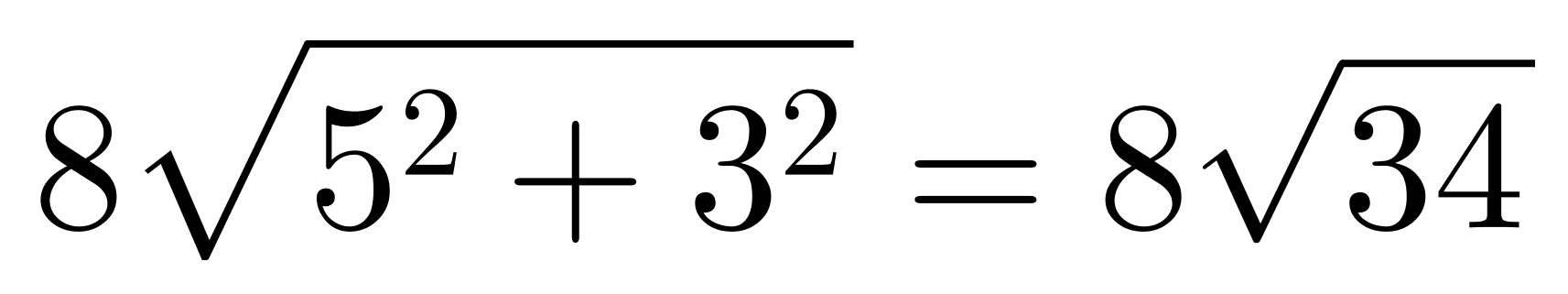、、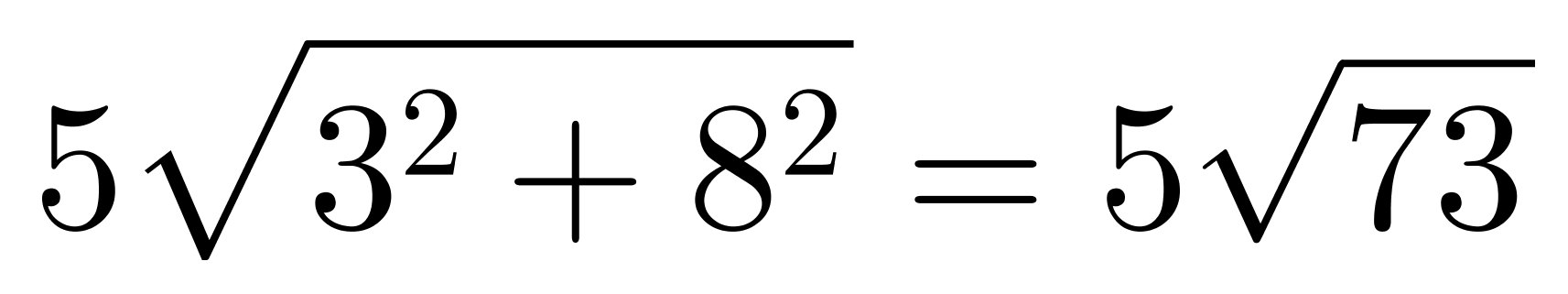，经比较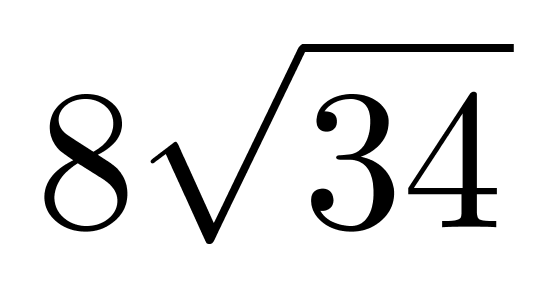最大。两个切面面积最大为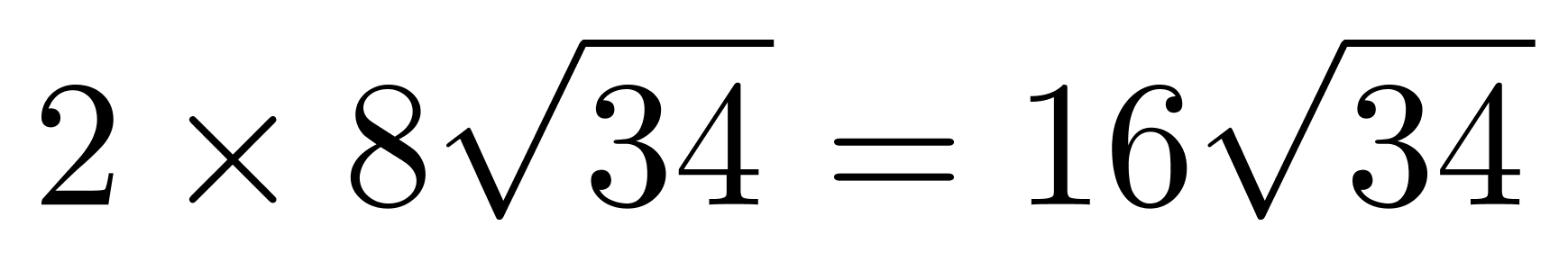（平方厘米）。
       
第三步，原长方体表面积为2×（8×5＋8×3＋5×3）＝158（平方厘米），故总表面积为（158＋16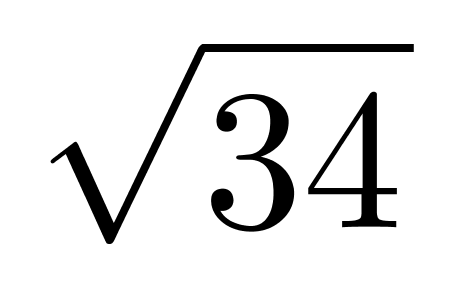）平方厘米。
因此，选择C选项。

3、

第一步，标记量化关系“和”、“是”。
       第二步，根据甲、乙、丙、丁面积“和”为，四边形ABCD的面积是，可知阴影部分面积为，则正方形EFGH面积为，故边长为，周长为。
       第三步，由图可知，甲、乙、丙、丁周长和应是正方形EFGH的2倍，故周长总和为。因此，选择C选项。
       

4、

       第一步，本题考查几何问题。
       第二步，B、D两部分均种了玫瑰花，故总面积为椭圆总面积的一半，椭圆的总面积介于大圆（直径16米）和小圆（直径12）之间，大圆和小圆的面积分别为π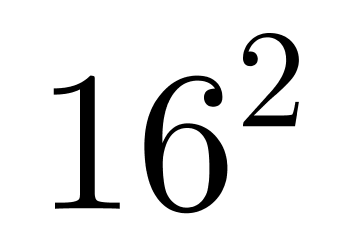/4=64π，和π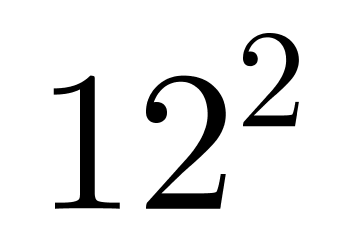/4=36π，椭圆总面积的一半介于18π和32π之间，观察选项只有24π符合。
       因此，选择A选项。
       

5、

第一步，标记量化关系“扇形”、“圆”。
       第二步，“扇形”的面积公式为：；“圆”的面积公式为：。故，解得。因此，选择D选项。

      ——相对面教育——

　　2023安徽事业单位招聘公告汇总

　　2023安徽省公务员考试职位查询

　　2023安徽事业单位联考职位查询

　　2023安徽省公务员课程辅导|备考资料